#include <iostream>
#ifdef _DEBUG
#ifndef DEBUG_NEW
#define DEBUG_NEW new(_NORMAL_BLOCK,__FILE__,__LINE__)
#define new DEBUG_NEW
#endif
#endif
using namespace std;
namespace _nmsp
{
template<typename T>
struct Double_Node
{
T data;
Double_Node<T>* prior;
Double_Node<T>* next;
};
template<typename T>
class Double_Link_List
{
public:
Double_Link_List();
~Double_Link_List();
public:
bool Double_Link_List_insert(int i, const T& e);
bool Double_Link_List_delete(int i);
bool Get_Elem(int i, T& e);
int Locate_Elem(const T& e);
void Display_Double_Link_List();
int Double_Link_List_length();
bool Empty();
private:
Double_Node<T>* m_head;
int m_length;
};
template<typename T>
Double_Link_List<T>::Double_Link_List()
{
m_head = new Double_Node<T>;
m_head->next = nullptr;
m_head->prior = nullptr;
m_length = 0;
}
template<typename T>
bool Double_Link_List<T>::Double_Link_List_insert(int i, const T& e)
{
if (i < 1 || i >(m_length + 1))
{
cout << "元素" << e << "插入的位置" << i << "不合法,合法的位置是1到" << m_length + 1 << "之间!" << endl;
return false;
}
Double_Node<T>* p_curr = m_head;
for (int j = 0; j < (i - 1); j++)
{
p_curr = p_curr->next;
}
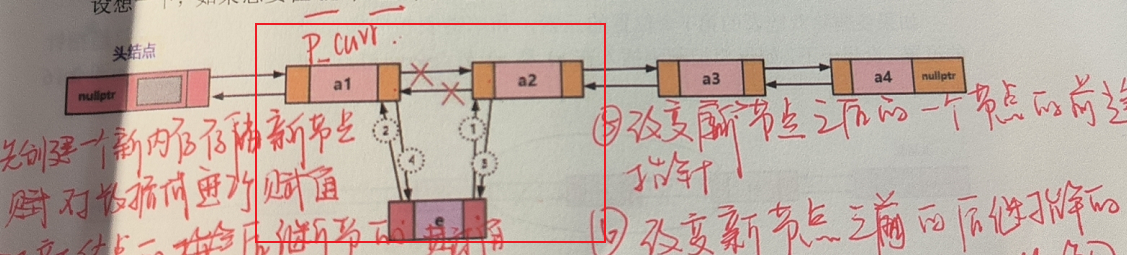
Double_Node<T>* node = new Double_Node<T>;
node->data = e;
node->next = p_curr->next;
node->prior = p_curr;
if (p_curr->next != nullptr)
{
p_curr->next->prior = node;
}
p_curr->next = node;
cout << "成功在位置为" << i << "处插入元素" << e << "!" << endl;
m_length++;
return true;
}
template<typename T>
bool Double_Link_List<T>::Double_Link_List_delete(int i)
{
if (m_length < 1)
{
cout << "当前双链表为空,不能删除任何数据!" << endl;
return false;
}
if (i < 1 || i > m_length)
{
cout << "删除的位置" << i << "不合法,合法的位置是1到" << m_length << "之间!" << endl;
return false;
}
Double_Node<T>* p_curr = m_head;
for (int j = 0; j < (i - 1); j++)
{
p_curr = p_curr->next;
}
Double_Node<T>* will_delete = p_curr->next
Double_Node<T>* will_delete_Next = will_delete->next;
p_curr->next = will_delete->next;
if (will_delete_Next != nullptr)
{
will_delete_Next->prior = p_curr;
}
cout << "成功删除位置为" << i << "的元素,该元素的值为" << will_delete->data << "!" << endl;
m_length--;
delete will_delete;
return true;
}
template<class T>
bool Double_Link_List<T>::Get_Elem(int i, T& e)
{
if (m_length < 1)
{
cout << "当前双链表为空,不能获取任何数据!" << endl;
return false;
}
if (i < 1 || i > m_length)
{
cout << "获取元素的位置" << i << "不合法,合法的位置是1到" << m_length << "之间!" << endl;
return false;
}
Double_Node<T>* p_curr = m_head;
for (int j = 0; j < i; ++j)
{
p_curr = p_curr->next;
}
e = p_curr->data;
cout << "成功获取位置为" << i << "的元素,该元素的值为" << e << "!" << endl;
return true;
}
template<class T>
int Double_Link_List<T>::Locate_Elem(const T& e)
{
Double_Node<T>* p_curr = m_head;
for (int i = 1; i <= m_length; ++i)
{
if (p_curr->next->data == e)
{
cout << "值为" << e << "的元素在双链表中第一次出现的位置为" << i << "!" << endl;
return i;
}
p_curr = p_curr->next;
}
cout << "值为" << e << "的元素在双链表中没有找到!" << endl;
return -1;
}
template<class T>
int Double_Link_List<T>::Double_Link_List_length()
{
return m_length;
}
template<class T>
bool Double_Link_List<T>::Empty()
{
if (m_head->next == nullptr)
{
return true;
}
return false;
}
template <typename T>
Double_Link_List<T>::~Double_Link_List()
{
Double_Node<T>* pnode = m_head->next;
Double_Node<T>* ptmp;
while (pnode != nullptr)
{
ptmp = pnode;
pnode = pnode->next;
delete ptmp;
}
delete m_head;
m_head = nullptr;
m_length = 0;
}
template<typename T>
void Double_Link_List<T>::Display_Double_Link_List()
{
Double_Node<T>* p = m_head->next;
while (p != nullptr)
{
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
}
int main()
{
_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);
_nmsp::Double_Link_List<int> Creat_D_L_List;
Creat_D_L_List.Double_Link_List_insert(1, 1);
Creat_D_L_List.Double_Link_List_insert(2, 2);
Creat_D_L_List.Double_Link_List_insert(3, 3);
Creat_D_L_List.Display_Double_Link_List();
Creat_D_L_List.Double_Link_List_length();
Creat_D_L_List.Double_Link_List_delete(1);
Creat_D_L_List.Display_Double_Link_List();
return 0;
}
|