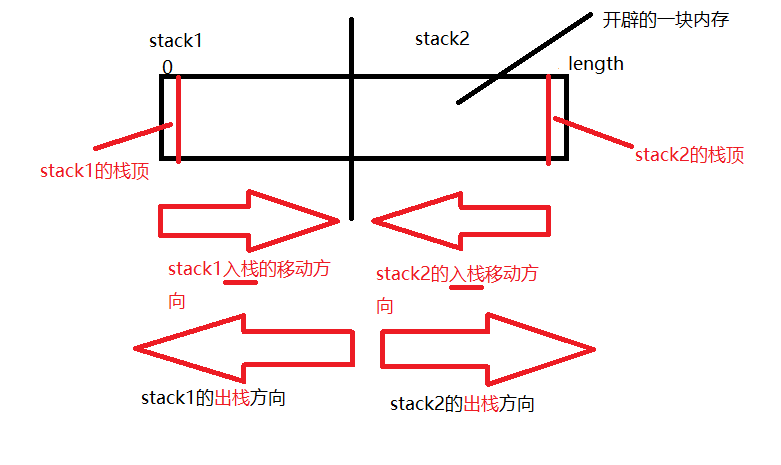
#include <iostream>
#ifdef _DEBUG
#ifndef DEBUG_NEW
#define DEBUG_NEW new(_NORMAL_BLOCK,__FILE__,__LINE__)
#define new DEBUG_NEW
#endif
#endif
using namespace std;
namespace _nmsp1
{
#define InitSize 10
#define IncSize 5
template <typename T>
class SeqStack
{
public:
SeqStack(int length = InitSize);
~SeqStack();
public:
bool Push(const T& e);
bool Pop(T& e);
bool GetTop(T& e);
void DispList();
int ListLength();
void IncreaseSize();
bool IsEmpty();
bool IsFull();
private:
T* m_data;
int m_maxsize;
int m_top;
};
template <typename T>
SeqStack<T>::SeqStack(int length)
{
m_data = new T[length];
m_maxsize = length;
m_top = -1;
}
template <typename T>
SeqStack<T>::~SeqStack()
{
delete[] m_data;
}
template <typename T>
bool SeqStack<T>::Push(const T& e)
{
if (IsFull() == true)
{
IncreaseSize();
}
m_top++;
m_data[m_top] = e;
return true;
}
template<class T>
void SeqStack<T>::IncreaseSize()
{
T* p = m_data;
m_data = new T[m_maxsize + IncSize];
for (int i = 0; i <= m_top; i++)
{
m_data[i] = p[i];
}
m_maxsize = m_maxsize + IncSize;
delete[] p;
}
template <typename T>
bool SeqStack<T>::Pop(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序栈为空,不能进行出栈操作!" << endl;
return false;
}
e = m_data[m_top];
m_top--;
return true;
}
template <typename T>
bool SeqStack<T>::GetTop(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序栈为空,不能读取栈顶元素!" << endl;
return false;
}
e = m_data[m_top];
return true;
}
template<class T>
void SeqStack<T>::DispList()
{
for (int i = m_top; i >= 0; --i)
{
cout << m_data[i] << " ";
}
cout << endl;
}
template<class T>
int SeqStack<T>::ListLength()
{
return m_top + 1;
}
template<class T>
bool SeqStack<T>::IsEmpty()
{
if (m_top == -1)
{
return true;
}
return false;
}
template<class T>
bool SeqStack<T>::IsFull()
{
if (m_top >= m_maxsize - 1)
{
return true;
}
return false;
}
int main()
{
_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);
_nmsp1::SeqStack<int> seqobj(10);
seqobj.Push(150);
seqobj.Push(200);
seqobj.Push(300);
seqobj.Push(400);
seqobj.DispList();
int eval = 0;
seqobj.Pop(eval);
seqobj.Pop(eval);
cout << "---------" << endl;
seqobj.DispList();
seqobj.Push(8100);
}
|